martes, marzo 21, 2006

 

Cómo demostrar la irracionalidad de un número


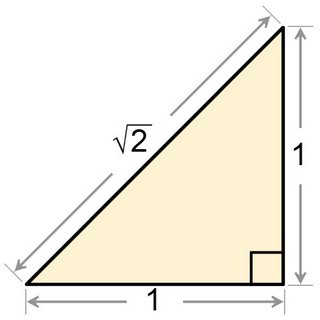
Hace unos días Viktor se preguntaba cómo puede saberse que un número del que sólo se han calculado un número finito de decimales es irracional, es decir, no puede expresarse de la forma p/q siendo p y q enteros, lo que implica que posee infinitas cifras decimales que no siguen ningún patrón repetitivo. Prometí entonces presentar una demostración sencilla de por qué un cierto número es irracional: el número raíz de 2. Lo escribiré como "sqrt(2)". Aquí está:

Supongamos que sqrt(2) es un número racional (ya véis que la demostración será por reducción al absurdo): sqrt(2)=p/q, donde p y q son números enteros. Podemos exigir que no tengan factores comunes (sin pérdida de generalidad), pues si los tuviesen bastaría con dividir cada uno de ellos por su máximo común divisor y los enteros resultantes ya no los tendrían y su cociente seguiría siendo igual a p/q. Entonces tenemos que 2=p2/q2, y por tanto (*):

p2=2q2.

Luego p2 es par (porque es igual a un número multiplicado por 2). Pero el cuadrado de cualquier número impar también es impar. Por lo tanto p también es par, es decir, p=2s para algún entero s.

Sustituyendo en en la ecuación (*) obtenemos: p2=(2s)2=4s2=2q2. Dividiendo por 2 en esta última igualdad: q2=2s2. Por tanto q2 también es par, luego (por lo mismo de antes) q también es par.

Pero si p y q son ambos números pares entonces ambos son divisibles por 2, lo cual contradice la hipótesis de que no tienen factores comunes. Luego por reducción al absurdo no existen p y q enteros tales que sqrt(2)=p/q. Por tanto sqrt(2) es irracional.

Espero que esta anotación no me haga perder demasiados lectores... :-)

Etiquetas:


Enlace permanente a esta anotación publicada por Javifields @ 17:24
comentarios:
Muy elegante. Con esta demostracion se puede decir eso de todas las potencias, pero que me dices de numeros como pi o e? ;) Me parece que si demuestras eso ya pierdes todas las visitas de tu blog :P
Comentario publicado por Blogger rmcantin : 21/3/06 18:04
 
jeje la de Pi no es tan fácil... puse un enlace a la más fácil que he encontrado en un comentario aquí
Comentario publicado por Blogger Javifields : 21/3/06 18:43
 
Bufff, te has pasado. ¿Sería posible explicarlo con peras y manzanas?
Comentario publicado por Anonymous Anónimo : 21/3/06 19:25
 
jajaja Jorgeras!!!!!! que haces perdiendo el tiempo con blogs!!! como ves este blog está en sus últimos estertores... no le doy ni una semana
Comentario publicado por Blogger Javifields : 21/3/06 19:28
 
recordatorio antes de que muera la bitacora de javifils:
me debes un post matematico acerca de la explicacion matemática de mi nombre (pi+n)
Comentario publicado por Blogger pin : 22/3/06 09:32
 
esta demostración no sale en el biggs ?
Comentario publicado por Anonymous Anónimo : 22/3/06 11:46
 
pues seguro, es la más conocida y fácil, sale en muchos sitios, hasta en wikipedia... mia desde luego no es! :-D
Comentario publicado por Blogger Javifields : 22/3/06 11:55
 
Asi da gusto estudiar matematicas hombre
Comentario publicado por Anonymous Anónimo : 22/3/06 20:47
 
Aquí hay otra demostración de lo mismo, acompañada de polámica
http://parafernaliasmatematicas.blogspot.com.es/2012/12/la-demostracion-de-apostol-de-la.html


Comentario publicado por Blogger filomates : 5/12/12 22:18
 
Publicar un comentario

<< Inicio