Allí andaban mis procesionarias del pino con sus problemillas de tráfico, ahora yo, ahora tu, con sus dimes y diretes, pero sin llegar a las manos.


Y llegó Pin a poner un poco de orden con sus protocolos y consejillos.


Y... ¿qué pasó? Pues pasó... pasó... os lo cuento al final.

Y yo me preguntaba, ¿cómo es posible que Pin con su mundo de colores (verde y fucsia, fundamentalmente) pueda armar el lío... el lío que veréis al final, con sólo unos consejillos inocentes?

Yo sabía de la irracionalidad de Pi. Y de la posible relación con el origen del nombre de Pin... ella misma me había dado pistas: que si Pin = Pi + n y lara lara lara...

Pero algo no cuadraba... como todos sabemos, sumando un número n a otro irracional (Pi) el resultado puede ser perfectamente racional si el número n también es irracional... y si el resultado, Pin, sale racional... ¿cómo iba a montar semejante lío... lío... el lío que veréis al final, con sólo un consejillo?

Pues bien, dí con la solución. Resulta que Pin no viene de Pi + n ("toma claro, le falta el signo +", diréis, pero a mi me costó varios días darme cuenta de ello), sino de


o lo que es lo mismo de aplicar la función Pi a n, es decir Pi(n).

¿Y qué es Pi(n)? Muy fácil: se llama la función cuenta primos.

Pi(n) se define como el número de números primos menores o iguales que n. Por ejemplo, Pi(1)=0, porque no hay primos menores o iguales que 1. Pi(2)=1, porque el 2 es primo. Pi(3)=2, porque el 2 y el 3 lo son. Etcétera. El nombre de la función no es muy afortunado, porque nada tiene que ver con el número Pi, pero es lo que hay; se lo dio un tal Edmund Landau en 1909 y con ese nombre se quedó la pobre función.

Y... ¿qué tiene que ver todo esto con nuestra Pin? Pues ahora veréis. Uno de los resultados fundamentales de teoría de números, que se llama nada menos que el teorema de los números primos, dice que la función Pi(n) es asintóticamente igual a la función Li(n), la función integral logarítmica. (¡Hala! Ahora todos a buscar el blog de el mundo de Lin, o el de Lin Consulting, a ver si existen). Casi me vais a perdonar que no escriba la definición de esta última función (podéis verla aquí), que si pocos lectores tengo ya, los perdería seguro.


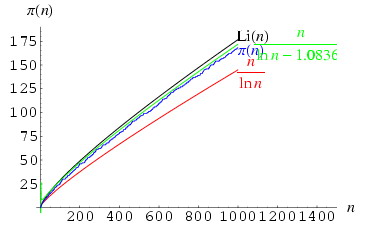
Como podéis ver, cuando n se hace grande, las dos funciones (la negra y la azul) crecen más o menos igual. Esto lo demostró Gauss en 1792, cuando tenía 15 añicos (¡qué tremendo el Gauss!).

A que esto es un lío. Pues eso. Eso es lo que tiene que ver con Pin. Así se quedaron mis oruguillas después de que Pin "pusiera un poco de orden":

Etiquetas: humor, varios