viernes, marzo 31, 2006
¡El sombrero!
Claro. Parece mentira. Mira que tengo para elegir...
Olvidé el sombrero y mi cabeza ardió.En fin, para algo habrá servido este craso error: para proveer de mi estupendo Snow-Hat a...
quien increiblemente no tenía gorro todavía en esta bitácora. Ya le tocaba.
Así le sienta el gorro a mi siempreviva.
Y éste es el modelo "Snow-Hat de Javifields para llevar", para que se lo lleve Damodar, si lo quiere:(Rmcantin: se te adelantó Damodar por muy poco; de momento te quedas sólo con tu Didjeridoo Gigante. Como vés el gorro obsequio no es mi gorro beige de montaña, que ese está en la montaña y no tengo fotos... queda para otra ocasión.)
Etiquetas: premios
jueves, marzo 30, 2006
¿Me olvido de algo?
Lala la lalala...Listo y equipado para un día en la nieve.
Ummmmm... ¿me olvido de algo?
Etiquetas: Sobrarbe
miércoles, marzo 29, 2006
µ: mariquitas en acción
El secreto vicio de mirar a otros.
¿Habías visto antes dos mariquitas en plena acción?
¿Habías visto antes dos mariquitas en plena acción?
Etiquetas: micra
martes, marzo 28, 2006
Florecicas: clavelina
El barranco de Sen es buen sitio para fotografiar flora y fauna pirenaica. Ya vimos un flamante lirio y una ranita, además del ibón.
Clavelina, barranco de Sen
Vemos ahora una Dianthus deltoides, de la familia de las cariofiláceas, vulgo clavelina o clavellina.
Aprovecho para poner el enlace del magnífico herbario de Jaca, propiedad del Instituto Pirenaico de Ecología (CSIC), con 8.000 especies vegetales y 350.000 muestras de toda Europa. Fundado en 1969 por el profesor Pedro Montserrat, es el tercero de España por su volumen y de particular interés por su especialización en Ecología.
Clavelina, barranco de SenVemos ahora una Dianthus deltoides, de la familia de las cariofiláceas, vulgo clavelina o clavellina.
Aprovecho para poner el enlace del magnífico herbario de Jaca, propiedad del Instituto Pirenaico de Ecología (CSIC), con 8.000 especies vegetales y 350.000 muestras de toda Europa. Fundado en 1969 por el profesor Pedro Montserrat, es el tercero de España por su volumen y de particular interés por su especialización en Ecología.
Etiquetas: florecicas, Sobrarbe
domingo, marzo 26, 2006
Foto: Panorámica de altura
De izquierda a derecha:
- El Cilindro (3.325 m),
- Monte Perdido (3.355 m),
- Soum de Ramond o Pico de Añisclo (3.259 m),
- Punta de las Olas (3.022 m),
- la hondonada central es el Collado de Añisclo (2.453 m), y luego
- La Suca (2.802 m),
- Las Tres Marías (2.781 m, 2.757 m, y 2.702 m, respectivamente),
- La Monesina (2.677 m) y
- Angonés (2.663 m).
viernes, marzo 24, 2006
Foto: emulando a Obelix
¿Alguna vez habéis construido un dolmen?No es nada fácil... salvo que te hayas caído de pequeño en una marmita de poción mágica.
Fotógrafo: XPhobos
miércoles, marzo 22, 2006
Pi n
Allí andaban mis procesionarias del pino con sus problemillas de tráfico, ahora yo, ahora tu, con sus dimes y diretes, pero sin llegar a las manos.
Y llegó Pin a poner un poco de orden con sus protocolos y consejillos.
Y... ¿qué pasó? Pues pasó... pasó... os lo cuento al final.
Y yo me preguntaba, ¿cómo es posible que Pin con su mundo de colores (verde y fucsia, fundamentalmente) pueda armar el lío... el lío que veréis al final, con sólo unos consejillos inocentes?
Yo sabía de la irracionalidad de Pi. Y de la posible relación con el origen del nombre de Pin... ella misma me había dado pistas: que si Pin = Pi + n y lara lara lara...
Pero algo no cuadraba... como todos sabemos, sumando un número n a otro irracional (Pi) el resultado puede ser perfectamente racional si el número n también es irracional... y si el resultado, Pin, sale racional... ¿cómo iba a montar semejante lío... lío... el lío que veréis al final, con sólo un consejillo?
Pues bien, dí con la solución. Resulta que Pin no viene de Pi + n ("toma claro, le falta el signo +", diréis, pero a mi me costó varios días darme cuenta de ello), sino de
o lo que es lo mismo de aplicar la función Pi a n, es decir Pi(n).
¿Y qué es Pi(n)? Muy fácil: se llama la función cuenta primos.
Pi(n) se define como el número de números primos menores o iguales que n. Por ejemplo, Pi(1)=0, porque no hay primos menores o iguales que 1. Pi(2)=1, porque el 2 es primo. Pi(3)=2, porque el 2 y el 3 lo son. Etcétera. El nombre de la función no es muy afortunado, porque nada tiene que ver con el número Pi, pero es lo que hay; se lo dio un tal Edmund Landau en 1909 y con ese nombre se quedó la pobre función.
Y... ¿qué tiene que ver todo esto con nuestra Pin? Pues ahora veréis. Uno de los resultados fundamentales de teoría de números, que se llama nada menos que el teorema de los números primos, dice que la función Pi(n) es asintóticamente igual a la función Li(n), la función integral logarítmica. (¡Hala! Ahora todos a buscar el blog de el mundo de Lin, o el de Lin Consulting, a ver si existen). Casi me vais a perdonar que no escriba la definición de esta última función (podéis verla aquí), que si pocos lectores tengo ya, los perdería seguro.
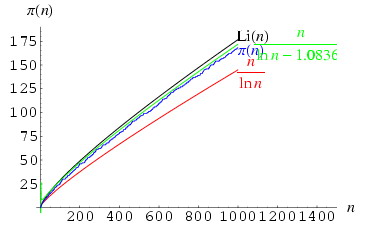
Como podéis ver, cuando n se hace grande, las dos funciones (la negra y la azul) crecen más o menos igual. Esto lo demostró Gauss en 1792, cuando tenía 15 añicos (¡qué tremendo el Gauss!).
A que esto es un lío. Pues eso. Eso es lo que tiene que ver con Pin. Así se quedaron mis oruguillas después de que Pin "pusiera un poco de orden":
Y llegó Pin a poner un poco de orden con sus protocolos y consejillos.
Y... ¿qué pasó? Pues pasó... pasó... os lo cuento al final.
Y yo me preguntaba, ¿cómo es posible que Pin con su mundo de colores (verde y fucsia, fundamentalmente) pueda armar el lío... el lío que veréis al final, con sólo unos consejillos inocentes?
Yo sabía de la irracionalidad de Pi. Y de la posible relación con el origen del nombre de Pin... ella misma me había dado pistas: que si Pin = Pi + n y lara lara lara...
Pero algo no cuadraba... como todos sabemos, sumando un número n a otro irracional (Pi) el resultado puede ser perfectamente racional si el número n también es irracional... y si el resultado, Pin, sale racional... ¿cómo iba a montar semejante lío... lío... el lío que veréis al final, con sólo un consejillo?
Pues bien, dí con la solución. Resulta que Pin no viene de Pi + n ("toma claro, le falta el signo +", diréis, pero a mi me costó varios días darme cuenta de ello), sino de
Pi n
o lo que es lo mismo de aplicar la función Pi a n, es decir Pi(n).
¿Y qué es Pi(n)? Muy fácil: se llama la función cuenta primos.
Pi(n) se define como el número de números primos menores o iguales que n. Por ejemplo, Pi(1)=0, porque no hay primos menores o iguales que 1. Pi(2)=1, porque el 2 es primo. Pi(3)=2, porque el 2 y el 3 lo son. Etcétera. El nombre de la función no es muy afortunado, porque nada tiene que ver con el número Pi, pero es lo que hay; se lo dio un tal Edmund Landau en 1909 y con ese nombre se quedó la pobre función.
Y... ¿qué tiene que ver todo esto con nuestra Pin? Pues ahora veréis. Uno de los resultados fundamentales de teoría de números, que se llama nada menos que el teorema de los números primos, dice que la función Pi(n) es asintóticamente igual a la función Li(n), la función integral logarítmica. (¡Hala! Ahora todos a buscar el blog de el mundo de Lin, o el de Lin Consulting, a ver si existen). Casi me vais a perdonar que no escriba la definición de esta última función (podéis verla aquí), que si pocos lectores tengo ya, los perdería seguro.
Como podéis ver, cuando n se hace grande, las dos funciones (la negra y la azul) crecen más o menos igual. Esto lo demostró Gauss en 1792, cuando tenía 15 añicos (¡qué tremendo el Gauss!).
A que esto es un lío. Pues eso. Eso es lo que tiene que ver con Pin. Así se quedaron mis oruguillas después de que Pin "pusiera un poco de orden":
martes, marzo 21, 2006
Cómo demostrar la irracionalidad de un número
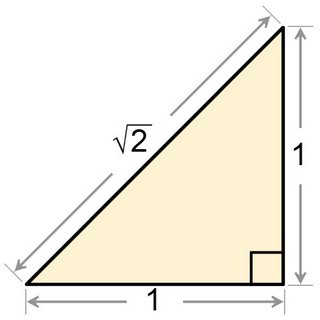
Hace unos días Viktor se preguntaba cómo puede saberse que un número del que sólo se han calculado un número finito de decimales es irracional, es decir, no puede expresarse de la forma p/q siendo p y q enteros, lo que implica que posee infinitas cifras decimales que no siguen ningún patrón repetitivo. Prometí entonces presentar una demostración sencilla de por qué un cierto número es irracional: el número raíz de 2. Lo escribiré como "sqrt(2)". Aquí está:
Supongamos que sqrt(2) es un número racional (ya véis que la demostración será por reducción al absurdo): sqrt(2)=p/q, donde p y q son números enteros. Podemos exigir que no tengan factores comunes (sin pérdida de generalidad), pues si los tuviesen bastaría con dividir cada uno de ellos por su máximo común divisor y los enteros resultantes ya no los tendrían y su cociente seguiría siendo igual a p/q. Entonces tenemos que 2=p2/q2, y por tanto (*):
p2=2q2.
Luego p2 es par (porque es igual a un número multiplicado por 2). Pero el cuadrado de cualquier número impar también es impar. Por lo tanto p también es par, es decir, p=2s para algún entero s.
Sustituyendo en en la ecuación (*) obtenemos: p2=(2s)2=4s2=2q2. Dividiendo por 2 en esta última igualdad: q2=2s2. Por tanto q2 también es par, luego (por lo mismo de antes) q también es par.
Pero si p y q son ambos números pares entonces ambos son divisibles por 2, lo cual contradice la hipótesis de que no tienen factores comunes. Luego por reducción al absurdo no existen p y q enteros tales que sqrt(2)=p/q. Por tanto sqrt(2) es irracional.
Espero que esta anotación no me haga perder demasiados lectores... :-)
Etiquetas: varios
domingo, marzo 19, 2006
Un punto azul pálido
[Dedicado a todos los nacionalistas de este planeta y a los de los otros planetas también.]
La Tierra desde 6.000 millones de Km de distancia
Ese puntito azul pálido es la Tierra. Así la captó el 14 de febrero de 1990 la cámara fotográfica de la nave espacial no tripulada Voyager 1. La V-1 se encontraba más allá de la órbita de Plutón y unos 32 grados por encima del plano de la eclíptica (plano de la órbita terrestre). La nave se alejaba de nosotros a 65.000 Km/h y recibió la orden (del conocido Mr. X) de volver su objetivo hacia aquí y captar 60 fotogramas, éste es uno de ellos.
La imagen constaba sólo de 640.000 píxeles. Cada uno de esos píxeles tardó cinco horas y media en recorrer, viajando a la velocidad de la luz desde la nave hasta la tierra, los seis mil millones de kilómetros de distancia.
El color azul se debe en parte al mar y en parte al cielo. El agua absorbe más la luz roja que la azul, por eso la luz que reflejan los oceános terrestres es azulada. Además, el aire de la atmósfera terrestre dispersa mucho mejor la luz azul que la roja, por eso desde muy lejos se intensifica el color azul reflejado por el mar. La palidez blanca del puntito azul se debe a que la tierra suele estar cubierta de nubes blancas, que matizan el reflejo azul. El reflejo de luz alrededor del punto es debido a los rayos del Sol.
La superficie total de ese puntito son unos 500 millones de kilómetros cuadrados. Los "terruños" por los que algunos terrícolas se parten la cara pueden suponer, con sus 10.000, 20.000 ó 30.000 Km2, menos de una diezmilésima parte de ese punto azul pálido.
La Tierra desde 6.000 millones de Km de distanciaEse puntito azul pálido es la Tierra. Así la captó el 14 de febrero de 1990 la cámara fotográfica de la nave espacial no tripulada Voyager 1. La V-1 se encontraba más allá de la órbita de Plutón y unos 32 grados por encima del plano de la eclíptica (plano de la órbita terrestre). La nave se alejaba de nosotros a 65.000 Km/h y recibió la orden (del conocido Mr. X) de volver su objetivo hacia aquí y captar 60 fotogramas, éste es uno de ellos.
La imagen constaba sólo de 640.000 píxeles. Cada uno de esos píxeles tardó cinco horas y media en recorrer, viajando a la velocidad de la luz desde la nave hasta la tierra, los seis mil millones de kilómetros de distancia.
El color azul se debe en parte al mar y en parte al cielo. El agua absorbe más la luz roja que la azul, por eso la luz que reflejan los oceános terrestres es azulada. Además, el aire de la atmósfera terrestre dispersa mucho mejor la luz azul que la roja, por eso desde muy lejos se intensifica el color azul reflejado por el mar. La palidez blanca del puntito azul se debe a que la tierra suele estar cubierta de nubes blancas, que matizan el reflejo azul. El reflejo de luz alrededor del punto es debido a los rayos del Sol.
La superficie total de ese puntito son unos 500 millones de kilómetros cuadrados. Los "terruños" por los que algunos terrícolas se parten la cara pueden suponer, con sus 10.000, 20.000 ó 30.000 Km2, menos de una diezmilésima parte de ese punto azul pálido.
¡Nacionalistas todos: introducíos en una nave interestelar, viajad bien lejos de este punto azul y luego hablamos!
Etiquetas: sociedad
jueves, marzo 16, 2006
µ: Problemas de tráfico
miércoles, marzo 15, 2006
Florecicas: rosas, margaritas y.... y... siempreviva
Dos de los regalos del 13-03. A la derecha: rosas (las blancas) y margaritas sin pétalos (las verdes). A la izquierda... a la izquierda... la llamaremos siempreviva, no hay que regarla, ni necesita luz, ni música ni nada. ¡Y sonríe siempre! Es un chollazo de planta.Etiquetas: florecicas
lunes, marzo 13, 2006
Sharbat Gula
Hace poco llegué no sé cómo a un post de Sansar y recordé lo que sigue.
La portada del número de junio de 1985 de la revista de National Geographic se convirtió desde el momento mismo de su publicación en una de las más famosas de la historia de la revista.
¿Por qué? Pues porque esa portada era la que véis abajo y esta mirada de ojos verdes impresionó a todos (podéis ampliar la foto con un click):
El fotógrafo, Steve McCurry, hizo la foto en junio de 1984 en el campamento de refugiados Nasir Bagh de Pakistán durante la guerra contra la invasión soviética. Nunca supo el nombre de la chica afgana refugiada, de unos 12 años de edad.
Tras una búsqueda de 17 años, McCurry la encontró de nuevo en 2001 y la volvió a fotografiar. Apareció en el número de la revista en noviembre de 2001.
Tenía entonces cerca de 30 años, había dado a luz a cuatro hijos, aunque uno murió al poco de nacer. Vivía alejada del mundo en una aldea de Afganistán sin saber que su cara se había hecho famosa y que su mirada había causado una conmoción mundial.
Cuando fotógrafo y modelo se vieron de nuevo, Sharbat Gula, que así se llama la mujer, dijo a McCurry que nadie más la había fotografiado nunca. Además, le contó que poco después de su encuentro en Pakistán en 1984, siendo adolescente, se casó y regresó a su país.
Su marido accedió a que Sharbat se quitase el burka y fuera fotografiada de nuevo por McCurry, y apareció otra vez en la portada de la revista National Geographic en abril de 2002.
Para National Geographic, Sharbat Gula se convertiría en símbolo de toda una generación de mujeres afganas, y la sociedad geográfica creó un fondo especial de ayuda al desarrollo y creación de oportunidades educativas para las niñas y mujeres afganas que puso en marcha con la colaboración de las autoridades locales y organizaciones sin ánimo de lucro.
Y ésta fue la historia de hoy. ¿Qué os sugiere?
La portada del número de junio de 1985 de la revista de National Geographic se convirtió desde el momento mismo de su publicación en una de las más famosas de la historia de la revista.
¿Por qué? Pues porque esa portada era la que véis abajo y esta mirada de ojos verdes impresionó a todos (podéis ampliar la foto con un click):
El fotógrafo, Steve McCurry, hizo la foto en junio de 1984 en el campamento de refugiados Nasir Bagh de Pakistán durante la guerra contra la invasión soviética. Nunca supo el nombre de la chica afgana refugiada, de unos 12 años de edad.
Tras una búsqueda de 17 años, McCurry la encontró de nuevo en 2001 y la volvió a fotografiar. Apareció en el número de la revista en noviembre de 2001.
Tenía entonces cerca de 30 años, había dado a luz a cuatro hijos, aunque uno murió al poco de nacer. Vivía alejada del mundo en una aldea de Afganistán sin saber que su cara se había hecho famosa y que su mirada había causado una conmoción mundial.
Cuando fotógrafo y modelo se vieron de nuevo, Sharbat Gula, que así se llama la mujer, dijo a McCurry que nadie más la había fotografiado nunca. Además, le contó que poco después de su encuentro en Pakistán en 1984, siendo adolescente, se casó y regresó a su país.
Su marido accedió a que Sharbat se quitase el burka y fuera fotografiada de nuevo por McCurry, y apareció otra vez en la portada de la revista National Geographic en abril de 2002.
Para National Geographic, Sharbat Gula se convertiría en símbolo de toda una generación de mujeres afganas, y la sociedad geográfica creó un fondo especial de ayuda al desarrollo y creación de oportunidades educativas para las niñas y mujeres afganas que puso en marcha con la colaboración de las autoridades locales y organizaciones sin ánimo de lucro.
Y ésta fue la historia de hoy. ¿Qué os sugiere?
Etiquetas: National Geographic, sociedad
sábado, marzo 11, 2006
Foto: aniversario
Kelantan significa textualmente la tierra de los relámpagos. Es tierra de arrozales, pueblecicos de pescadores y playas de arena blanca, en el noreste de Malasia, justo debajo de Tailandia. Está gobernada desde hace años por el Partido Islámico.Al final, lo que va dentro de los trenes o autobuses de aquí o de allá es lo mismo, gente como tú o como yo, gente como ésta.
Fotógrafo: Javifields
Etiquetas: fotos, Malasia, música, sociedad
jueves, marzo 09, 2006
¿Mala memoria?
¿Te has olvidado de cómo sigue esa canción, ese poema o esa novela?Teclea las primeras palabras y dale a "start".
by Douwe Osinga
Etiquetas: informática
miércoles, marzo 08, 2006
Animalicos: coatí
Ésta es mi fiera para enfrentarse al Zepelín de WiZoo. No me gusta apostar para perder.
Coatí, en el bosque nuboso de Monteverde, Costa Rica
También conocido con los nombres comunes de coatimundi, pizote o cuzumbo, es parecido a un mapache. Mamífero carnicero plantígrado, americano, de cabeza alargada y hocico estrecho con nariz muy saliente y puntiaguda, orejas cortas y redondeadas y pelaje largo y tupido. Tiene uñas fuertes y encorvadas que le sirven para trepar a los árboles.
El mismo coatí sigue buscando una banana
Y esas uñas fuertes le sirven para lanzar tremendos zarpazos hacia cualquier cosa que lleves en la mano pensando que puede ser algo para echarse a la boca. Así que si llevas una banana no te acerques demasiado.
El bosque nuboso de Monteverde es famoso por el quetzal y por los tremendos hojones que crecen en él. Y hay otros bichos aparte del quetzal y del coatí, como puede verse...
Haciendo el mico
Coatí, en el bosque nuboso de Monteverde, Costa RicaTambién conocido con los nombres comunes de coatimundi, pizote o cuzumbo, es parecido a un mapache. Mamífero carnicero plantígrado, americano, de cabeza alargada y hocico estrecho con nariz muy saliente y puntiaguda, orejas cortas y redondeadas y pelaje largo y tupido. Tiene uñas fuertes y encorvadas que le sirven para trepar a los árboles.
El mismo coatí sigue buscando una bananaY esas uñas fuertes le sirven para lanzar tremendos zarpazos hacia cualquier cosa que lleves en la mano pensando que puede ser algo para echarse a la boca. Así que si llevas una banana no te acerques demasiado.
El bosque nuboso de Monteverde es famoso por el quetzal y por los tremendos hojones que crecen en él. Y hay otros bichos aparte del quetzal y del coatí, como puede verse...
Haciendo el micoEtiquetas: animalicos, Costa Rica
martes, marzo 07, 2006
µ: La sed insaciable
Tengo tanta sed que me bebería una gota de agua entera... Vaya, que tengo una sed de hormiga.
Decir adiós... La vida es eso.
Y yo te digo adiós, y sigo...
Volver a amar es el castigo
de los que amaron con exceso.
Amar y amar toda la vida,
y arder en esa llama.
Y no saber por qué se ama...
Y no saber por qué se olvida...
Coger las rosas una a una,
beber un vino y otro vino,
y andar y andar por un camino
que no conduce a parte alguna.
Sentir más sed en cada fuente
y ver más sombra en cada abismo,
en este amor que es siempre el mismo,
pero que siempre es diferente.
Porque en sordo desacuerdo
de lo soñado y lo vivido,
siempre, del fondo del olvido,
nace la muerte de un recuerdo.
Y en esta angustia que no cesa,
que toca el alma y no la toca,
besar la sombra de otra boca
en cada boca que se besa.
(La sed insaciable, José Ángel Buesa)
Y yo te digo adiós, y sigo...
Volver a amar es el castigo
de los que amaron con exceso.
Amar y amar toda la vida,
y arder en esa llama.
Y no saber por qué se ama...
Y no saber por qué se olvida...
Coger las rosas una a una,
beber un vino y otro vino,
y andar y andar por un camino
que no conduce a parte alguna.
Sentir más sed en cada fuente
y ver más sombra en cada abismo,
en este amor que es siempre el mismo,
pero que siempre es diferente.
Porque en sordo desacuerdo
de lo soñado y lo vivido,
siempre, del fondo del olvido,
nace la muerte de un recuerdo.
Y en esta angustia que no cesa,
que toca el alma y no la toca,
besar la sombra de otra boca
en cada boca que se besa.
(La sed insaciable, José Ángel Buesa)
Etiquetas: micra
domingo, marzo 05, 2006
Frases de cine: Apuesto por...
Me la juego. A pocas horas de la ceremonia de entrega de los premios, apuesto por...
La película de hoy: Brokeback Mountain
Título original: Brokeback Mountain
Director: Ang Lee
Año: 2005
IMDB: más información
Brokeback Mountain (Ang Lee, 2005)
El director ya nos ha dado alguna muestra previa de buen hacer (El banquete de boda, 1992; Comer, beber, amar, 1994; Tigre y dragón, 2000) y ésta es sin duda su mejor obra hasta el momento. Los actores, prácticamente desconocidos, hacen un trabajo excelente (ambos nominados) pero si hay que destacar algo es la dirección. No me extrañaría que Lee se llevase también ese premio.
No es "una de vaqueros" y tampoco es justo simplificarla como "una de gays". Es simplemente un muy buen drama romántico, rodado con un estilo y contención propios de un director oriental.
El resumen sería el mismo válido para la película Los puentes de Madison, de Eastwood: Dos personas se enamoran y en medio se interpone... la vida (P. Kurt, Filmaffinity).
Escenas entre Heath Ledger (Ennis Del Mar) y Jake Gyllenhaal (Jack Twist):
J.G.: ¿Qué hacemos ahora?
H.L.: No creo que podamos hacer nada, ya estoy pillado con lo que tengo aquí.
J.G.: ¿Hasta cuándo?
H.L.: Hasta que aguantemos, aquí no llevamos las riendas.
La película de hoy: Brokeback Mountain
Título original: Brokeback Mountain
Director: Ang Lee
Año: 2005
IMDB: más información
Brokeback Mountain (Ang Lee, 2005)El director ya nos ha dado alguna muestra previa de buen hacer (El banquete de boda, 1992; Comer, beber, amar, 1994; Tigre y dragón, 2000) y ésta es sin duda su mejor obra hasta el momento. Los actores, prácticamente desconocidos, hacen un trabajo excelente (ambos nominados) pero si hay que destacar algo es la dirección. No me extrañaría que Lee se llevase también ese premio.
No es "una de vaqueros" y tampoco es justo simplificarla como "una de gays". Es simplemente un muy buen drama romántico, rodado con un estilo y contención propios de un director oriental.
El resumen sería el mismo válido para la película Los puentes de Madison, de Eastwood: Dos personas se enamoran y en medio se interpone... la vida (P. Kurt, Filmaffinity).
Escenas entre Heath Ledger (Ennis Del Mar) y Jake Gyllenhaal (Jack Twist):
J.G.: ¿Qué hacemos ahora?
H.L.: No creo que podamos hacer nada, ya estoy pillado con lo que tengo aquí.
J.G.: ¿Hasta cuándo?
H.L.: Hasta que aguantemos, aquí no llevamos las riendas.
Etiquetas: cine
viernes, marzo 03, 2006
Foto: un hotel cutre cutre cutre
Hay hoteles cutrecillos, hoteles realmente cutres... y luego está el Gran Hotel Imperial de San José de Costa Rica.Dijo el taxista al llegar, "no paséis de aquella calle, es la muerte".
Podría decirse por tanto que está a menos de una cuadra de la muerte.
Fotógrafo: Luis
[EDITADO el 5/3/06] Exekias no va desencaminado en su comentario. La habitación se parece a ésta:
Munich, Steven SpielbergEtiquetas: Costa Rica, fotos
jueves, marzo 02, 2006
Javifields' law revisited
¿Os acordais de la ley de Javifields?
Nadie creyó demasiado en ella, pero yo sabía que tendría algunas consecuencias importantes.
Aquí están:
¡Hala! Ahí queda eso.
Nadie creyó demasiado en ella, pero yo sabía que tendría algunas consecuencias importantes.
Aquí están:
¡Hala! Ahí queda eso.
Etiquetas: humor
en la zona VIP de UGDM
saamis de los Manitoba
calcetín de Pin
botijo de Chencho
